Học cách tính Thể tích khối trụ tròn xoay với ví dụ minh họa

Việc tính thể tích khối trụ tròn xoay là kiến thức rất quan trọng trong cả học tập và kiểm tra. Bài toán thể tích khối trụ tròn xoay thường xuyên xuất hiện, không chỉ trong môi trường học tập mà còn trong ứng dụng thực tế. Để bạn có thể hiểu rõ hơn về công thức và cách áp dụng, Mytour sẽ cung cấp cho bạn Công thức và Ví dụ cụ thể.

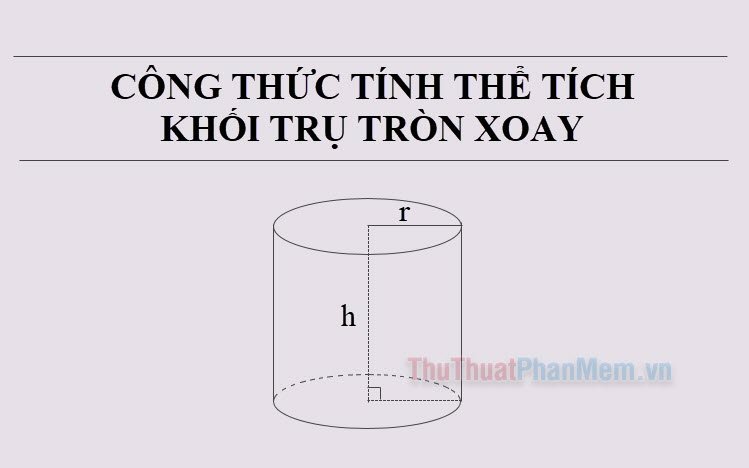
1. Đặc điểm của Khối trụ tròn xoay

Khối tròn xoay được tạo ra bằng cách xoay một hình phẳng quanh một trục cố định. Hình trụ tròn xoay hình thành từ việc quay một hình chữ nhật quanh trục cố định của nó.

Khối trụ tròn xoay là sự kết hợp hài hòa giữa một hình trụ và không gian trong lòng nó. Thể tích của khối trụ tròn xoay biểu thị phần không gian mà hình trụ chiếm giữ trong không gian 3D.

Những đặc điểm chính của khối trụ tròn xoay bao gồm:

• Đế của khối trụ là một hình tròn, chuyển thành mặt bên khi khối trụ quay quanh trục
• Trục của khối trụ là đường thẳng đi qua trung tâm của đế, là trục quay của hình tròn khi hình thành khối trụ tròn xoay
• Mặt bên của khối trụ là các vòng tròn song song với đế, tạo thành bề mặt cong của khối trụ
• Chiều cao của khối trụ tròn xoay là khoảng cách từ mặt đế đến mặt đỉnh của khối trụ.

2. Công thức tính thể tích khối trụ tròn xoay

Để tính thể tích của một khối trụ tròn xoay, bạn cần lấy diện tích của đáy hình tròn và nhân với chiều cao của khối trụ. Chỉ cần nhân diện tích đáy với chiều cao, bạn sẽ có thể tính được thể tích của khối trụ tròn xoay.

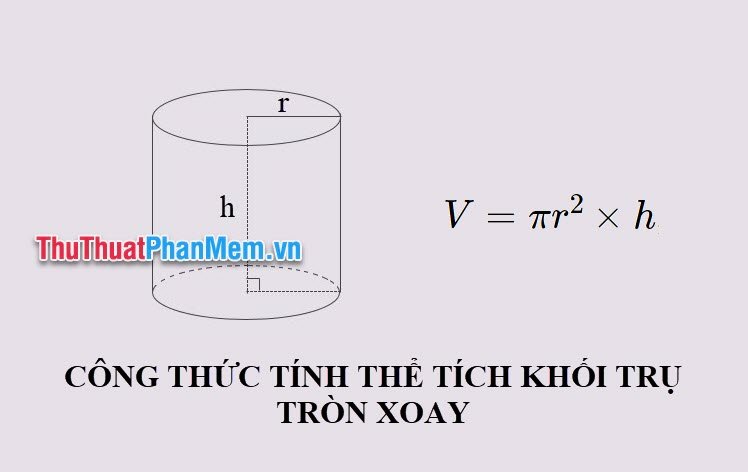
Công thức để tính thể tích khối trụ tròn xoay là: V=Sa×h=πr2×h$V=S_a\times h=\pi r^2\times h$

Trong đó:

• V là thể tích khối trụ tròn xoay
• π là hằng số Pi, có giá trị khoảng 3.14159
• r là bán kính của hình tròn cơ sở của khối trụ (bán kính của đáy)
• h là chiều cao của khối trụ tròn xoay

3. Ví dụ minh họa

Ví dụ 1: Cho khối trụ tròn xoay có bán kính r = 5 cm và chiều cao h = 12 cm. Tính thể tích của khối trụ tròn xoay?

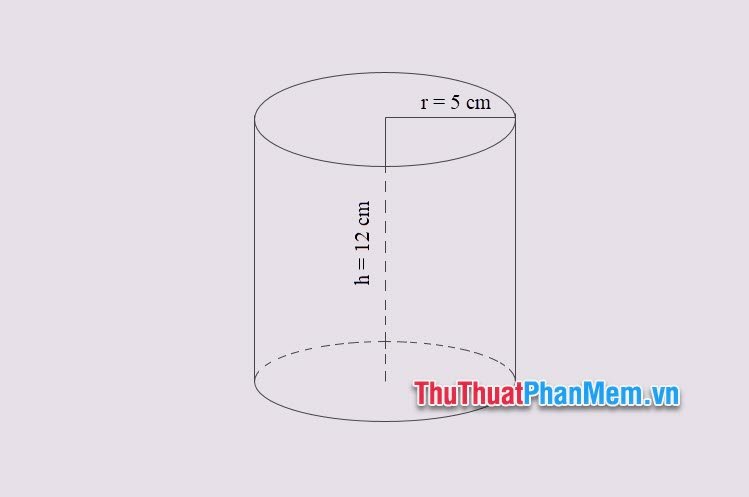
Lời giải

Chúng ta áp dụng công thức tính thể tích khối trụ tròn xoay V=πr2×h$V=\pi r^2\times h$, ta có:

V=π×52×12=π×300≈942,478 cm3$V=\pi \times 5^2\times 12=\pi \times 300\approx 942,478{cm}^3$

Vậy thể tích của khối trụ tròn xoay xấp xỉ bằng 942,478 cm3$942,478{cm}^3$

Ví dụ 2: Cho khối trụ tròn xoay có đáy là hình tròn ngoại tiếp tam giác đều cạnh a. Biết chiều cao của khối trụ là 3a. Tính thể tích khối trụ tròn xoay đó?

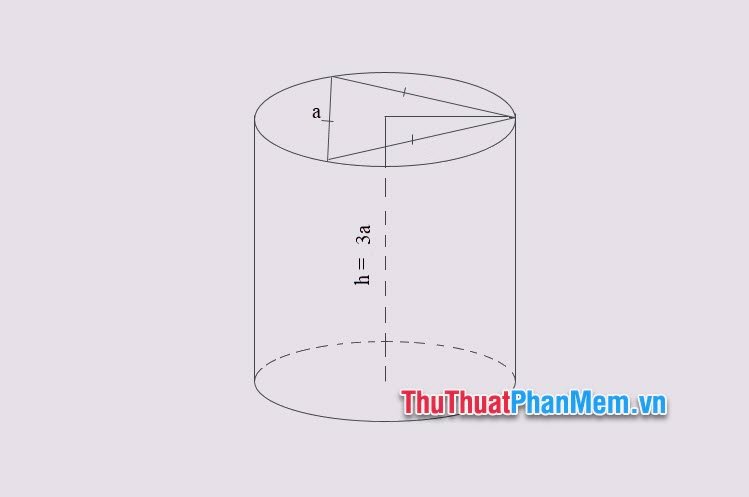
Lời giải

Hình tròn đáy là hình tròn ngoại tiếp của một tam giác đều cạnh a, nên dựa theo định lý sin ta có bán kính của hình tròn đó là

R=a2sin60∘=a2√32=a√33$R=\frac{a}{2\sin {60}^{\circ }}=\frac{a}{2\frac{\sqrt{3}}{2}}=\frac{a}{\sqrt{3}}=\frac{a\sqrt{3}}{3}$

Chúng ta áp dụng công thức tính thể tích khối trụ tròn xoay để có thể đưa ra như sau:

V=πr2×h=π(a√33)2×3a=π×3a)a9×3a=πa)π2mi=π×π<>mi=rmi>)>(msqrx(mi>a>3>mnah3<(math)=mathmlms)mn3am<>(msupactions>mfractions&><)。/trmπ<>msup><>math>><>><>Mas>